ALU

L'ALU, che sta per Arithmetic Logic Unit, ha lo scopo di eseguire operazioni aritmetiche e logiche come and, or, add, beq, etc.

Somma

La somma di due numeri a 32 bit sulla ALU è formata da 1 bit adder (una serie da 32) con la tabella di verità:

dove $R_i$ è il riporto precedente, $S$ è la somma e $R_o$ è il riporto dell'operazione.

Minimizzando la tabella si arriva ad avere che: $$\begin{gathered} S=\neg AB\neg R_i+A\neg B\neg R_i+\neg A\neg B{R}_i+AB{R}_i \\ {R}_o=AB+B{R}_i+A{R}_i \end{gathered}$$ ma dato che $S$ non è semplificabile, si possono usare le porte XOR, infatti:

e quindi: $$\begin{gathered} S=(A\oplus B)\oplus R_i \\ {R}_o=AB+(A\oplus B)R_i \end{gathered}$$

Sottrazione

Utilizzando il complemento a due e l'adder è possibile ottenere una somma, dato che: $$A-B=A+(-B)=A+(\neg B+1)$$

Di conseguenza basterà fare la somma tra $A$ e $\neg B$, mettendo il riporto entrante $R_i=1$, in modo da considerare anche il $+1$.

Confronto

Un'altra funzione della ALU è quella di confronto, che servirà poi per implementare l'istruzione slt: $$Op=3\wedge A<B\Rightarrow R=1$$

Lo stato del confronto si può ottenere dalla ALU sul MSB (Most Significant Bit) da cui viene letto il bit di segno della sottrazione tra $A$ e $B$, con gli appropriati resti: $$A-B<0\Rightarrow A<B\Rightarrow S=1$$ dove il valore di $S$ verrà usato come input per $L$ (cioè less) sulla prima ALU in modo che $R=1\vee R=0$, visto che il numero $1$ ha solo il LSB (Least Significant Bit) attivo.

Questo però non funziona se $A>0$ e $B<0$, perchè $A+(-B)$ è una somma tra due numeri positivi che può portare ad overflow, cosa che potrebbe dare un $S$ errato per cui il risultato $R$ sarebbe sbagliato.

ALU da 1 bit

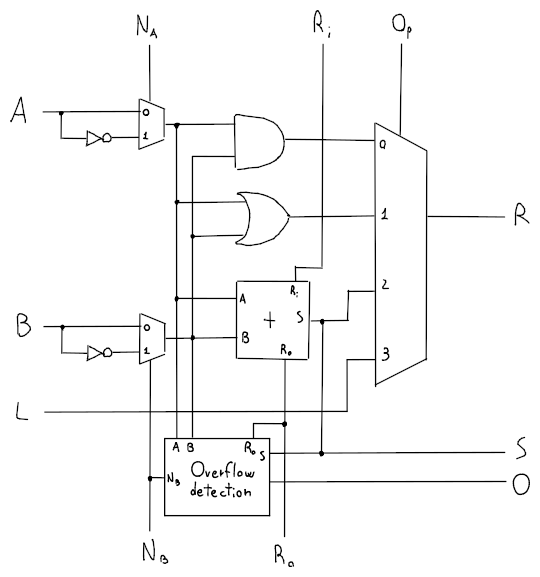
dove:

• $A$, $B$ sono gli input della ALU
• $N_A$, $N_B$, sono dei flag con cui si decide se usare la versione negativa di $A$ o di $B$ come input
• $R_i$ è il riporto precedente, mentre $R_o$ è il riporto di output
• $Op$ indica quale operazione vogliamo dalla ALU
• $R$ è il risultato dell'operazione
• $L$, $S$ sono usati internamente per la condizione $A<B$
• $O$ indica l'overflow della somma

Quindi è possibile riassumere le operazioni in:

e visto che non ci interessa lo stato $R_i$ per il NOR, è possibile porre $R_i=N_B$ sulla prima 1 bit ALU nella catena delle ALU.

ALU da 32 bit

Per ricavare la ALU da 32 bit basta concatenare le varie ALU da 1 bit per ogni bit della word.

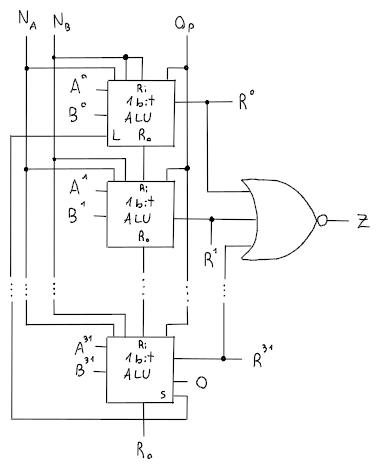
dove $Z$ equivale al NOR tra tutti i bit di output e sarà $1$ quando $R=0$.

Questa ALU però, avrà performance abbastanza lente, perchè ogni riporto di ogni 1 bit adder dovrà propagarsi per tutta la catena di 1 bit ALU, cosa che rallenterà il segnale. Per migliorare le prestazioni quindi, esiste un metodo chiamato Carry Lookahead.

Moltiplicazione

Questa parte non sarà contenuta all'interno dell'ALU ma la sfrutterà per creare l'algoritmo che permette la moltiplicazione tra due numeri.

L'algoritmo si basa sul metodo di moltiplicazione in colonna e si può riassumere in:

long mul(int a, int b) {
	unsigned long r0 = abs(a);	// Registro a 64bit perchè r0 << 1 per 32 volte
	unsigned int r1 = abs(b);

	long sum = 0;
	for (size_t i = 0; i < sizeof(a) * 8; i++) {
		if (r1 & 0x1) {
			sum += r0;	// Necessaria una ALU da 64bit
		}
		r0 <<= 1;
		r1 >>= 1;
	}

	if ((a > 0) ^ (b > 0)) {	// Controllo dei bit di segno
		sum = -sum;
	}

	return sum;	// a * b
}

che necessita, però, di una ALU e di un registro a 64bit, motivo per cui è stato ideato un algoritmo alternativo che è anche più ottimizzato:

long mul(int a, int b) {
	unsigned int r1 = abs(b);

	long sum = 0;
	for (size_t i = 0; i < sizeof(a) * 8; i++) {
		if (r1 & 0x1) {
			unsigned int upper = sum >> (sizeof(sum)*8/2);
			unsigned int lower = sum & ~0U;

			upper += abs(a);
			sum = (long) upper << (sizeof(sum)*8/2) | lower;
		}
		r1 >>= 1;
		sum >>= 1;
	}

	if ((a > 0) ^ (b > 0)) {
		sum = -sum;
	}

	return sum;
}