Proprietà locali
Una funzione può essere crescente o decrescente localmente rispetto ad un punto .
Può quindi soddisfare le proprietà locali:
-
Crescente: cioè se esiste un intorno per cui l'immagine dell'intorno sinistro di (dentro ) è minore del valore , e l'immagine dell'intorno destro di è maggiore di .
-
Decrescente: cioè, analogamente a quando è crescente, se esiste un intorno per cui l'immagine dell'intorno sinistro di è maggiore del valore , e l'immagine dell'intorno destro di è minore di .
-
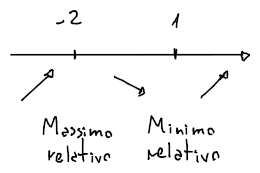
Massimo relativo:
-
Minimo relativo:
I massimi e minimi dipendono anche dal dominio di , infatti se un minimo relativo sarà su , ma se si restringe il dominio su allora diventerà minimo e sarà assoluto.
Si dicono assoluti (quindi se hanno asintoni orizzontali) se si può determinare che:
Studio del segno della derivata
In base al segno della derivata di sul punto si può determinare le proprietà che rispetta :
-
e quindi rispetta la proprietà locale per cui è crescente in , ma strettamente, di conseguenza -
-
se è un punto interno al .In base a come tende il grafico della funzione intorno a , si può determinare che:
- Se crescente a sinistra di e decrescente a destra, allora è un massimo locale
- Se decrescente a sinistra di e crescente a destra, allora è un minimo locale
- Se crescente intorno a , allora è un punto di flesso a tangente orizzontale
- Se decrescente intorno a , allora è un punto di flesso a tangente orizzontale
Esempio
Sia , non ci sono massimi e minimi assoluti perchè: ma ce ne sono di relativi, infatti: per cui, essendo positivo in si ha che: