Problema SAT

Il problema SAT cerca l'esistenza di un istanza che porti un'espressione logica ad essere vera. Analogamente, il problema del CIRCUIT-SAT cerca l'input che porti un circuito logico a restituire $1$.

Entrambi sono NP completi, e vengono detti soddisfacibili quando possiedono un'istanza positiva.

Per esempio, l'espressione $(x_1\vee \neg x_2)\wedge (\neg x_1\vee x_2)\wedge (x_1\vee x_2)$ è soddisfacibile con $x_1=x_2=1$.

Forma normale congiunta

Nell'algebra booleana è più comodo usare formule in forma canonica, o forma normale congiunta (FNC).

In questa forma, la struttura è suddivisa in $q$ clausole ognuna composta da $k$ letterali: $$\Phi =(l_1\vee ...\vee l_k)\wedge C_2\wedge ...\wedge C_q$$

In particolare, il formato $k$-FNC sono quelle espressioni che hanno $k$ letterali su ogni clausola.

Classe della clique

Si può dimostrare che il problema della clique $\mathcal{P}$ è NP completo, infatti si riconosce da:

1. $\mathcal{P}\in \mathrm{NP}$, perchè è verificabile in $O(n^2)$ se ogni coppia di nodi ha un arco

2. Il problema SAT-3FNC, cioè il SAT in formato $3$-FNC, è riducibile a $\mathcal{P}$
   Questo è dimostrabile perchè una qualunque sua istanza come $$\Phi =(x_1\vee \neg x_2\vee \neg x_3)\wedge (\neg x_1\vee x_2\vee x_3)\wedge (x_1\vee x_2\vee x_3)$$ è trasformabile in un grafo, creando un nodo per ogni letterale, escludendo:

   • gli archi tra letterali della stessa clausola
   • archi tra letterali opposti

   con cui si ottiene il grafo:

   

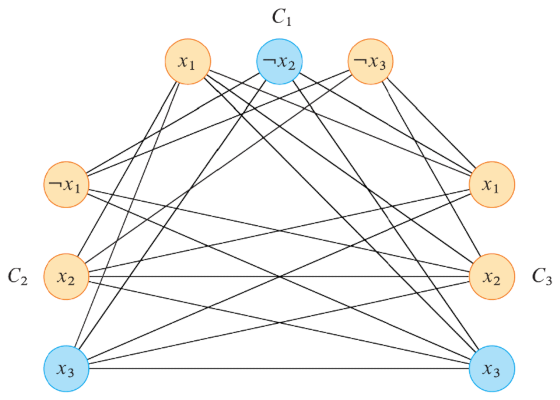
   Di conseguenza, l'espressione $\Phi$ è soddisfacibile sse esiste una clique da $3$ nodi, infatti se si pongono a $1$ i nodi blu della clique scelta si ottengono $x_2=0$, $x_3=1$ e $x_1$ arbitrario, che soddisfano $\Phi$.

Gestire problemi intrattabili

Per poter gestire problemi NP completi si può ricorrere a:

1. Algoritmi di approssimazioni: trovano una soluzione, meno un errore $ϵ$, in tempo polinomiale
2. Gestire solo i casi speciali, sperando che il problema ne rientri
3. Affidarsi ad euristiche: tentano di trovare la soluzione senza certezze