Convessità, concavità e flessi

Derivate di ordine superiore

Una funzione $f$ può essere derivata più di una volta: $$f^{(k)}=(f^{(k-1)}{)}^{\prime }=\frac{d^{k}f}{d{x}^k}$$ dove l'indice $k\in \mathbb{N}$ indica l'ordine di derivazione.

Classi di funzioni derivabili

Una funzione $f$ si dice di classe $C^k$ se le sue derivate esistono fino a $f^{(k)}$ e l'ultima è continua, di conseguenza si ha che $f\in C^k(I)$ con: $$C^k(I)=\{f:I\to \mathbb{R}|f\text{ derivabile }k\text{ volte e }{f}^{(k)}\text{ continua}\}$$

Se $f\in C^0$ allora $f$ si dice continua, ma se $f\in C^1$ allora $f$ è continua, differenziabile e $f^{\prime }$ è continua.

Convessità e concavità

Una funzione si dice convessa se per ogni coppia di punti $x_1,x_2\in I$, la retta secante su $x_1$ e $x_2$ si trova al di sopra del grafico di $f$ e quindi la concavità è rivolta verso l'alto: $$f(x)\le \frac{f(x_2)-f(x_1)}{x_2-x_1}(x-x_1)+f(x_1),\forall x\in ]x_1,x_2[$$ dove il membro a destra corrisponde all'equazione della retta secante $y=m(x-x_1)+y_1$.

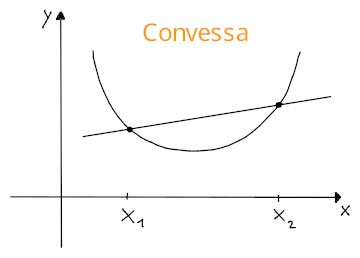
Una funzione si dice concava invece, se la retta secante $g$ si trova al di sotto del grafico di $f$, e quindi $f(x)\ge g(x),\forall x\in ]x_1,x_2[$ per cui la concavità è rivolta verso il basso.

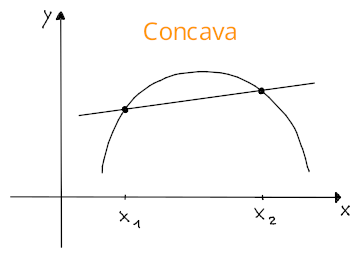
Attraverso $f^{\prime \prime }$ è possibile determinare la concavità, se:

• $f^{\prime \prime }(x)\ge 0,\forall x\in I$, allora $f$ è convessa in $I$
• $f^{\prime \prime }(x)\le 0,\forall x\in I$, allora $f$ è concava in $I$

Convessità e concavità locale e punti di flesso

Una funzione si dice localmente convessa in $x_0$ se: $$\exists \delta >0:f(x)\ge f^{\prime }(x_0)(x-x_0)+f(x_0),\forall x\in B(x_0,\delta )$$ cioè quando le immagini dei punti di un intorno circolare di $x_0$ stanno sopra i punti della tangente in $x_0$. Al contrario della convessità di $f$ su un intervallo, i punti stanno sopra la retta perchè è tangente di $x_0$ e quindi ha una sola intersezione.

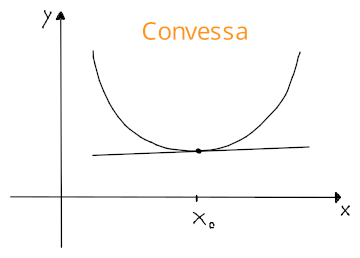
Si dice localmente concava in $x_0$ invece, se sono i punti sulla retta ad essere più grandi di $f(x)$ nell'intorno.

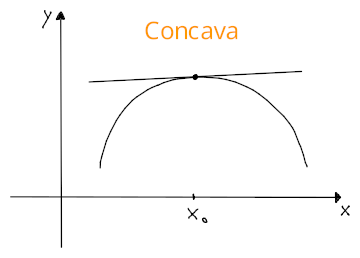
Il punto $x_0$ si dice punto di flesso per $f$ se esiste $\delta >0$ tale che $f$ è localmente convessa a sinistra di $x_0$ e localmente concava a destra, o viceversa.

Anche in questo caso, è possibile determinarlo attraverso $f^{\prime \prime }$, se:

• $f^{\prime \prime }(x_0)>0$, allora $f$ è convessa in $x_0$
• $f^{\prime \prime }(x_0)<0$, allora $f$ è concava in $x_0$
• $f^{\prime \prime }(x_0)=0$, allora $x_0$ è punto di flesso, cioè di cambio di concavità