Intervalli

Un intervallo $I$ (e.g. $[0,2]$) si può definire come $\forall x,y\in I:x\le y\Rightarrow z\in I,\forall z\in \mathbb{R}:x\le z\le y$, e cioè che tra qualunque coppia di punti arbitrari $x$ e $y$ (con $x\le y$) dentro $I$, ci saranno infiniti punti $z\in \mathbb{R}$ tra $x$ e $y$ inclusi in $I$.

Alcuni tipi di combinazioni di intervalli possono essere:

• $(a,b)$ o $]a,b[$: limitato, aperto
• $[a,b]$: limitato, chiuso
• $[a,b)$: limitato, chiuso a sinistra e aperto a destra
• $(a,+\infty )$: illimitato superiormente e aperto a sinistra
• $(-\infty ,b]$: illimitato inferiormente e chiuso a destra
• $(-\infty ,+\infty )$: illimitato (e uguale ad $\mathbb{R}$)
• $[a,a]=\{a\}$
• $(a,a)=[a,a)=(a,a]=\varnothing$

Intorni

Dato un punto $p\in \mathbb{R}$, si chiamerà intorno di $p$ o $I(p)$ un qualunque insieme aperto $A\subset \mathbb{R}$, che contenga il punto $p$.

Avendo un raggio $r>0$:

• $B(p,r)=(p-r,p+r)$ si chiamerà intorno circolare aperto di $p$
• $(p-r,p)$ sarà l'intorno sinistro di $p$
• $(p,p+r)$ sarà l'intorno destro di $p$

Intorno sinistro e destro però, non sono considerabili dei veri e propri intorni, perchè $p$ non ne è contenuto.

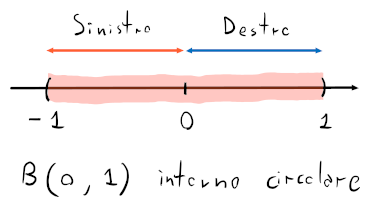
Inoltre, chiamiamo $\overline{B}(p,r)=[p-r,p+r]$ intorno circolare chiuso di $p$.

Insiemi aperti e chiusi

Un insieme $A$ è un insieme aperto, quando $A=\mathring{A}$ e cioè che ogni elemento possiede un intorno circolare contenuto in $A$.

L'insieme è considerato insieme chiuso, quando $F(A)\subseteq A$ e cioè quando contiene tutti i suoi punti di frontiera. Equivalentemente, $A$ è considerato chiuso, anche quando $A^C$ è aperto.

Proprietà

• $\varnothing$ è l'unico insieme ad essere sia aperto che chiuso

• Con $A,B$ aperti, $A\cup B$ e $A\cap B$ sono aperti

• ${\bigcup }_{n=1}^{+\infty }{A}_n$, cioè l'unione di infiniti intervalli, è aperta

• ${\bigcap }_{n=1}^{+\infty }{A}_n$, cioè l'intersezione di infiniti intervalli, può non essere aperta

  Per esempio, con $n\in \mathbb{N}$:

  $$\bigcap _{n=1}^{+\infty }\left(-\frac{1}{n},\frac{1}{n}\right)=A_1\cap A_2\cap ...\cap A_n=\{0\}=[0,0]$$

  Che dimostra che l'intersezione di infiniti intervalli che diventano sempre più piccoli su $0$ è $\{0\}$.

• Con $A,B$ chiusi, $A\cup B$ e $A\cap B$ sono chiusi

• ${\bigcap }_{n=1}^{+\infty }{A}_n$, cioè l'intersezione di infiniti intervalli, è aperta

• ${\bigcup }_{n=1}^{+\infty }{A}_n$, cioè l'unione di infiniti intervalli, può non essere chiusa

  Per esempio, con $n\in \mathbb{N}$:

  $$\bigcup _{n=1}^{+\infty }\left[-n,n\right]=A_1\cup A_2\cup ...\cup A_n=\mathbb{R}$$

  Che dimostra che l'unione di infiniti intervalli che diventano sempre più grandi è $\mathbb{R}$, che è aperto.

Teorema di Cantor

Dati $I_n$ intervalli chiusi e limitati, tale che $I_{n+1}\subseteq I_n$ allora $\exists c\in \mathbb{R}:c\in {\bigcap }_{n=1}^{+\infty }{I}_n$.

Inoltre, se l'ampiezza di $I_n$ tende a diminuire con l'aumento di $n$, allora ${\bigcap }_{n=1}^{+\infty }{I}_n=\{c\}$, con $c\in \mathbb{R}$.

Punti interni ed esterni

Un punto $x$ si dice interno ad un intervallo $A$ se $x\in A$ e $\exists r>0:B(x,r)\subset A$, di conseguenza $\sup (A)$ e $\inf (A)$ non sono considerabili come punti interni ad $A$.

Un punto $x$ è detto esterno invece, se $\exists r>0:B(x,r)\subset A^C$ cosa che, anche in questo caso, esclude gli estremi.

Il simbolo $\mathring{A}$ corrisponde all'insieme di tutti i punti interni ad $A$.

Punti di frontiera

Un punto $x$ si dice di frontiera o $F(A)$, ad un intervallo $A$ se $\exists y\in A,\exists z\in A^C:y,z\in B(x,r),\forall r>0$, cioè che la palla $B(x,r)$ includerà sia alcuni punti di $A$, che alcuni punti di $A^C$, e di conseguenza $x$ non è né interno né esterno, ma di frontiera tra $A$ e il suo complementare.

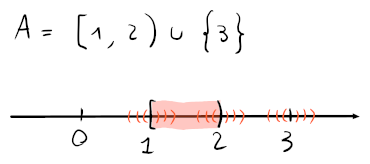
Per esempio, in un insieme $A=[1,2)\cup \{3\}$ i punti di frontiera saranno $F(A)=\{1,2,3\}$, dato che su tutti i punti gli intorni circolari contengono elementi di $A$ e $A^C$.

In particole il punto di frontiera su $3$, avrà l'intorno sinistro e destro contenuti in $A^C$, e un singolo punto (su $3$) contenuto in $A$.

Punti di accumulazione e isolati

Un punto $x$ si dice di accumulazione per $A$ se per ogni intorno di $x$ è presente almeno un punto di $A$, e quindi ci sono infiniti punti intorno ad $x$ appartenenti ad $A$.

Nel caso in cui un punto non sia di accumulazione, allora si chiamerà punto isolato.

Per esempio, su $A=[1,2)\cup \{3\}$ i punti di accumulazione sono tutti i punti su $[1,2]$, mentre il punto su $3$ sarà un punto isolato. Il punto $2$ è incluso perchè $\forall r>0,B(2,r)$ contiene infiniti punti di $A$ a sinistra.