Complessità asintotica

La complessità asintotica di un algoritmo descrive l'andamento temporale per input di grandezza $n\to \infty$.

Sequenza di Fibonacci

Per esempio, data la sequenza di Fibonacci definita come $$F_n=\{\begin{array}{ll}1& \text{se }n=1,2\\ F_{n-1}+F_{n-2}& \text{se }n\ge 3\end{array}$$ esistono diversi algoritmi per trovare l'$n$-esimo numero:

Binet

La formula di Binet lega la sezione aurea all'$n$-esimo numero di Fibonacci: $$F_n=\frac{1}{\sqrt{5}}\left({\phi }^n-{\hat{\phi }}^n\right)$$ dove $\phi$ e $\hat{\phi }$ sono le soluzioni a $x^2=x+1$.

Di conseguenza, l'algoritmo risulta semplicemente essere:

Fib1(int n) -> int
	return 1/sqrt(5) * (pow(phi, n) - pow(1 - phi, n))

Complessità temporale e spaziale

In questo caso, $T(n)\approx S(n)\approx 1$ dato che l'algoritmo è composto da un return e l'unico dato salvato è $n$.

Correttezza

Per verificane la correttezza, bisogna dimostrare che: $$F_n=\frac{1}{\sqrt{5}}({\phi }^n-{\hat{\phi }}^n)$$

Proseguendo per induzione, i casi base sono:

• Per $n=1$, $$\frac{1}{\sqrt{5}}({\phi }^1-{\hat{\phi }}^1)=\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}-1+\sqrt{5}}{2}\right)=1=F_1$$
• Per $n=2$, $$\frac{1}{\sqrt{5}}({\phi }^2-{\hat{\phi }}^2)=\frac{1}{\sqrt{5}}\left(\frac{1+2\sqrt{5}+5-1+2\sqrt{5}-5}{4}\right)=1=F_2$$

Per cui va verificato il passo induttivo: $$F_{n-1}+F_{n-2}=\frac{1}{\sqrt{5}}({\phi }^n-{\hat{\phi }}^n)$$ di conseguenza, dati i casi base, si suppone che la formula sia valida per $F_{n-1}$ e $F_{n-2}$, per cui: $$\begin{array}{rl}{F}_{n-1}+F_{n-2}& =\frac{1}{\sqrt{5}}({\phi }^{n-1}-{\hat{\phi }}^{n-1})+\frac{1}{\sqrt{5}}({\phi }^{n-2}-{\hat{\phi }}^{n-2})=\frac{1}{\sqrt{5}}({\phi }^{n-1}-{\hat{\phi }}^{n-1}+{\phi }^{n-2}-{\hat{\phi }}^{n-2})\\ & =\frac{1}{\sqrt{5}}(({\phi }^{n-1}+{\phi }^{n-2})-({\hat{\phi }}^{n-1}+{\hat{\phi }}^{n-2}))\end{array}$$ che va trasformata in $\frac{1}{\sqrt{5}}({\phi }^n-{\hat{\phi }}^n)$, cioè: $$\{\begin{array}{l}{\phi }^n={\phi }^{n-1}+{\phi }^{n-2}\\ {\hat{\phi }}^n={\hat{\phi }}^{n-1}+{\hat{\phi }}^{n-2}\end{array}\iff \{\begin{array}{l}\frac{{\phi }^n}{{\phi }^{n-2}}=\frac{{\phi }^{n-1}}{{\phi }^{n-2}}+1\\ \frac{{\hat{\phi }}^n}{{\hat{\phi }}^{n-2}}=\frac{{\hat{\phi }}^{n-1}}{{\hat{\phi }}^{n-2}}+1\end{array}\iff \{\begin{array}{l}{\phi }^2=\phi +1\\ {\hat{\phi }}^2=\hat{\phi }+1\end{array}$$ e siccome $\phi$ e $\hat{\phi }$ sono le uniche soluzioni del sistema, la formula è verificata.

Seppur dimostrato, Fib1 rimane incorretto perchè l'imprecisione aumenta con il crescere di $n$.

Ricorsivo

Nel caso ricorsivo, l'algoritmo risulta essere:

Fib2(int n) -> int
	if n <= 2
		return 1
	return Fib2(n - 1) + Fib2(n - 2)

Complessità temporale e spaziale

I passaggi che fa questo algoritmo sono: $$T(n)=\{\begin{array}{ll}1& \text{se }n=1,2\\ 2+T(n-1)+T(n-2)& \text{se }n\ge 3\end{array}$$ dove $1$ è per l'if/return, mentre $2$ è per l'if più l'else/return.

Per trovare il valore di $T(n)$ si può usare un albero ricorsivo $T_n$. Per $n=5$, l'albero $T_5$ sarà:

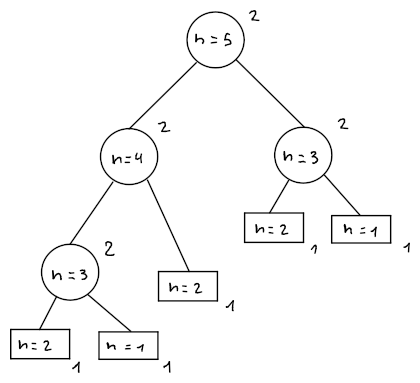
Contando i pesi sui nodi dell'albero, si può ricavare il costo: $$T(n)=2\cdot 4+1\cdot 5=2\cdot i(T_n)+f(T_n)$$ dove $i(T_n)$ è il numero di nodi interni e $f(T_n)$ è il numero di foglie.

Si può quindi dimostrare che:

1. $f(T_n)=F_n$, per induzione:

   Tra i casi base, se:

   • $n=1\Rightarrow f(T_1)=1=F_1$
   • $n=2\Rightarrow f(T_2)=1=F_2$

   Per cui, supponendo che $f(T_{n-1})=F_{n-1}\wedge f(T_{n-2})=F_{n-2}$ sia vero per ipotesi induttiva, allora: $$f(T_n)=f(T_{n-1})+f(T_{n-2})$$ dato che $T_n$ non possiede altri sottoalberi oltre che $T_{n-1}$ e $T_{n-2}$. Di conseguenza: $$f(T_n)=F_{n-1}+F_{n-2}=F_n$$

2. $i(T_n)=f(T_n)-1=F_n-1$

   Tra i casi base, se:

   • $n=1\Rightarrow i(T_1)=0=F_1-1=f(T_1)-1$
   • $n=2\Rightarrow i(T_2)=0=F_2-1=f(T_2)-1$

   Supponendo $i(T_{n-1})=f(T_{n-1})-1\wedge i(T_{n-2})=f(T_{n-2})-1$ vero per ipotesi induttiva, allora: $$\begin{array}{rl}i(T_n)& =i(T_{n-1})+i(T_{n-2})+1=\\ & =f(T_{n-1})-1+f(T_{n-2})-1+1=\\ & =f(T_n)-1\end{array}$$ visto che per la precedente dimostrazione $f(T_n)=f(T_{n-1})+f(T_{n-2})$.

Perciò, la complessità temporale di Fib2 sarà: $$T(n)=2\cdot (F_n-1)+F_n=3F_n-2\approx F_n$$ e la complessità spaziale $S(n)\approx n$.

È anche possibile che la complessità cresce più velocemente che esponenzialmente: $$F_n\ge 2^{\frac{n}{2}},\forall n\ge 6$$ infatti per induzione, il caso base per $n=6\Rightarrow F_6\ge 2^3$ e il passo induttivo per $n>6$: $$\begin{gathered} F_n=\stackrel{\ge 2^{\frac{n-1}{2}}}{\overbrace{F_{n-1}}}+\stackrel{\ge 2^{\frac{n-2}{2}}}{\overbrace{F_{n-2}}} \\ \Downarrow \\ \begin{array}{rl}{F}_n& \ge 2^{\frac{n-1}{2}}+2^{\frac{n-2}{2}}\\ & \ge 2^{\frac{n}{2}}\cdot 2^{-\frac{1}{2}}+2^{\frac{n}{2}}\cdot 2^{-1}\\ & \ge 2^{\frac{n}{2}}\left(\underset{\ge 1}{\underbrace{\frac{1}{\sqrt{2}}+\frac{1}{2}}}\right)\ge 2^{\frac{n}{2}}\end{array} \end{gathered}$$

Iterativo con array

Sfruttando un array, si possono salvare i valori di $F_n$ senza doverli ricalcolare su $F_{n+1}$:

Fib3(int n) -> int
	int F[n]
	F[1] = F[2] = 1
	for i = 3 to n
		F[i] = F[i-1] + F[i-2]
	return F[n]

Complessità temporale e spaziale

Il numero di istruzioni eseguite sono $$T(n)=3+(n-3+1)+(n-3+1+1)=2n\approx n$$ dove $3$ sono per l'inizializzazione di F e il return, mentre:

• $n-3+1$ sul contenuto del ciclo: eseguito per $i=3$ e per il resto delle $n-3$ volte
• $n-3+1+1$ sulla condizione: per $i=3$, per il resto delle $n-3$ volte e una alla fine per $i=n+1$

Mentre lo spazio occupato sarà $S(n)\approx n$, dato che viene salvato $F_n$ per ogni $n$.

Iterativo

La precedente versione si può ottimizzare ulteriormente, salvando solamente $F_{n-1}$ e $F_{n-2}$:

Fib4(int n) -> int
	int f1 = 1, f2 = 1, f
	for i = 3 to n
		f = f1 + f2
		f1 = f2
		f2 = f
	return f

per cui rimane che $T(n)=4n-5\approx n$, mentre la complessità spaziale diventa $S(n)\approx 1$.