Operazioni

• Addizione: $$a+b=(a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2+b_2)$$

  

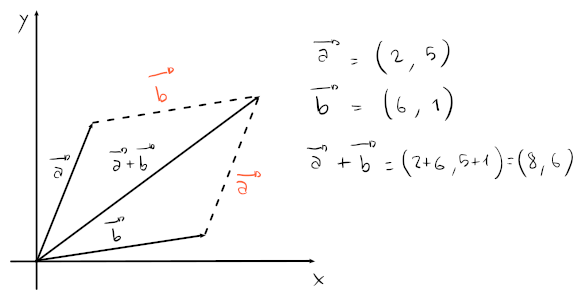
• Prodotto per uno scalare $c\in \mathbb{R}$: $$c\cdot a=c\cdot (a_1,a_2)=(c\cdot a_1,c\cdot a_2)$$

  

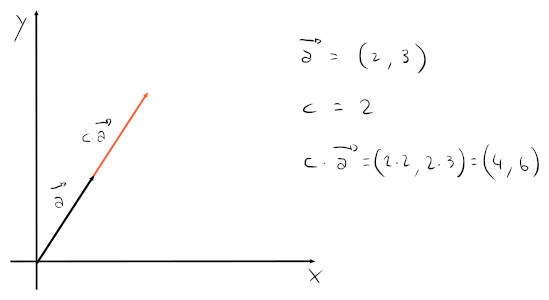
• Norma, o modulo: $$||v||=\sqrt{v\cdot v}=\sqrt{(v_1{)}^2+(v_2{)}^2}$$ dove $v\cdot v$ corrisponde al prodotto scalare tra $v$ e se stesso, cioè a $||v|{|}^2$.

• Prodotto scalare: $$v\cdot w=(||v||\cdot \cos (\alpha ))\cdot ||w||$$ dove $\alpha$ corrisponde all'angolo tra i due vettori $v$ e $w$.

  La parte $||v||\cos (\alpha )$ si può pensare come la proiezione di $v$ su $w$, che poi servirà come scalare per $||w||$, ridimensionando quindi la lunghezza di $w$ secondo la lunghezza della proiezione.

  

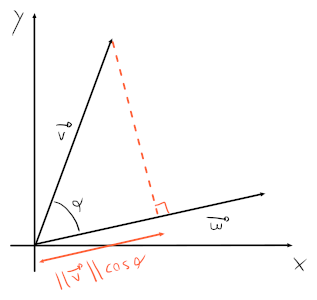
  Un modo più veloce per moltiplicare due vettori però, senza conoscere $\alpha$, è: $$a\cdot b=(a_1,a_2)\cdot (b_1,b_2)=a_1{b}_1+a_2{b}_2$$

  Della moltiplicazione valgono le seguenti proprietà:

  • $a\cdot b=b\cdot a$
  • $a\cdot (b+c)=a\cdot b+a\cdot c$
  • $(c\cdot a)\cdot b=c\cdot (a\cdot b)$, con $c\in \mathbb{R}$
  • Se $a=0$ allora $a\cdot a=0$, altrimenti $a\cdot a>0$

Tutte le operazioni possono essere generalizzate su $n$ dimensioni.
Per esempio, $||v||=||\sqrt{({\sum }_{i=1}^n(v_i{)}^2)}||$, su ${\mathbb{R}}^n$.

Vettore unità

Un vettore unità $\tilde{v}$, è un vettore la cui norma è uguale ad $1$.

Per ottenere il vettore unità su un vettore $v$, basta ridimensionare la norma in modo che sia $1$dividendo per il valore scalare $||v||$: $$\tilde{v}=\frac{v}{||v||}$$

Per esempio, se $v=(2,3)$ allora $\tilde{v}=\frac{v}{\sqrt{13}}=\left(\frac{2}{\sqrt{13}},\frac{3}{\sqrt{13}}\right)$.

Distanza tra due punti

Per trovare la distanza tra due punti, basta: $$\mathrm{dist}(A,B)=||\overrightarrow{AB}||=||B-A||=\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}$$

Per esempio, se $C=(-2,1)$ e $D=(2,1)$, $\overrightarrow{CD}=(x_D-x_C,y_D-y_C)=(4,0)$, quindi $||\overrightarrow{CD}||=4$.