Tipi di funzione

Una funzione $$\begin{array}{rl}f:& A\to B\\ & x\mapsto y=f(x)\end{array}$$

si dice:

• Suriettiva, se tutti i punti del codominio si possono ricavare da $f(x)$, e quindi se $\mathrm{Im}(f)=B$: $$\forall y\in B,\exists x\in A:y=f(x)$$

• Iniettiva, se per ogni $x$ esiste massimo una sola $f(x)$: $$\forall x_1,x_2\in A,f(x_1)=f(x_2)\Rightarrow x_1=x_2$$

• Biettiva, se la funzione è sia suriettiva che iniettiva

Esempio

Sia $f$ la funzione $f:\mathbb{R}\to \mathbb{R}:x\mapsto y=x^2$.

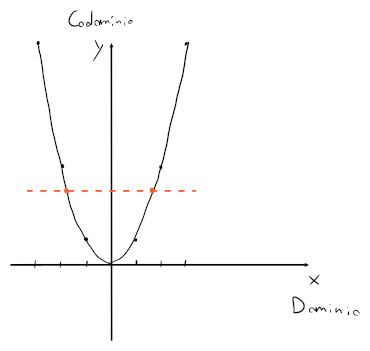
La parabola quindi non è suriettiva perchè ci sono dei punti del codominio che non fanno parte di $\mathrm{Im}(f)$ (i.e. $y<0$), ma neanche iniettiva perchè esistono delle $x$ diverse per cui $f(x)$ restituisce lo stesso risultato (i.e. i due punti arancioni).

Restrizioni di funzioni

Restringere una funzione può portarla a diventare suriettiva o iniettiva. Questo è possibile cambiando il suo dominio e codominio.

Per la parabola $y=x^2$, essa diventa iniettiva se si restringe il suo dominio a $D=[0,+\infty )$ (espressa come $f_{|D}$), mentre diventa suriettiva se si restringe il suo codominio a $C=[0,+\infty )$.

Funzioni monotone

Una funzione viene chiamata monotona quando soddisfa una delle seguenti proprietà:

• Crescente, se $f(x)\le f(z),\forall x,z\in D:x<z$
• Decrescente se $f(x)\ge f(z),\forall x,z\in D:x<z$
• Strettamente crescente se $f(x)<f(z)$
• Strettamente decrescente se $f(x)>f(z)$
• Costante, se $|f(D)|=1$ e quindi $f(x)=f(z)$ (e.g. le rette orizzontali)

Funzioni simmetriche

Una funzione si dice simmetrica, quando è:

• $f(-x)=f(x)$ o pari, per cui è simmetrica rispetto all'asse $y$
• $f(-x)=-f(x)$ o dispari, per cui è simmetrica rispetto all'origine

Per esempio, $|x|$ è pari e $x^3$ è dispari.

Funzioni periodiche

Una funzione $f:D\to \mathbb{R}$, è detta periodica quando $\exists ϵ>0:\forall x\in D,x\pm ϵ\in D\wedge f(x\pm ϵ)=f(x)$, cioè quando i valori immagine della funzione si ripetono ogni valore arbitrario $ϵ$. Il più piccolo $ϵ$ esistente rappresenta il periodo della funzione $f$.

Per esempio, $\sin (x)$ ha periodo $\pi$ e $y=c$ con $c\in \mathbb{R}$ ha periodo $ϵ,\forall ϵ>0$.