Integrali definiti

L'integrale definito, $${\int }_a^{b}f(x)dx$$ serve per calcolare l'area del trapezoide tra il grafico di $f$, l'asse $x$ e $x=a$ e $x=b$.

L'area può essere approssimata attraverso dei plurirettangoli:

• Plurirettangoli inscritti:

  Per cui l'area è approssimata dalla somma delle aree dei rettangoli inscritti nel grafico sottostante a $f$: $$I\approx s_n=\sum _{i=1}^n{h}_i\Delta x$$ dove $\Delta x=\frac{b-a}{n}$ è la base dei rettangoli, mentre $h_i=\underset{x\in I_i}{\min }(f(x))$, con $I_i$ che è l'intervallo sulle $x$ largo $\Delta x$, è l'altezza del rettangolo $i$-esimo.

• Plurirettangoli circoscritti

  Per cui è approssimata dai rettangoli inscritti: $$I\approx S_n=\sum _{i=1}^n{H}_i\Delta x$$ dove $H_i=\underset{x\in I_i}{\max }(f(x))$.

Per il teorema del confronto, $\sup (s_n)=\inf (S_n)=I$ e quindi: $$\begin{array}{rcccl}{s}_n& \le & I& \le & S_n\\ & \searrow & \stackrel{n\to +\infty \Rightarrow \Delta x\to 0}{\downarrow }& \swarrow & \\ & & {\int }_a^{b}f(x)dx& & \end{array}$$

Esempio

$${\int }_0^{3}x+2dx=\frac{(5+2)\cdot 3}{2}$$ perchè la funzione $f(x)=x+2$ da $0$ a $3$ forma un trapezio.

Si ha che $\Delta x=\frac{3-0}{n}=\frac{3}{n}$ dove $n$ è il numero di plurirettangoli tra $0$ e $3$.
Ogni plurirettangolo ha intervallo $I_i=[x_{i-1},x_i]$, dove $x_i=x_{i-1}+\Delta x=x_0+i\cdot \Delta x=i\Delta x$.

Quindi la somma degli integrali superiori sarà: $$\begin{array}{rl}{S}_n& =\sum _{i=1}^n\Delta xf(x_i)=\\ & =\sum _{i=1}^n\frac{3}{n}\left(\frac{3}{n}\cdot i+2\right)=\\ & =\frac{9}{n^2}\sum _{i=1}^{n}i+\frac{6}{n}\sum _{i=1}^{n}1=\\ & =\frac{9}{n^2}\cdot \frac{n(n+1)}{2}+\frac{6}{n}\cdot n=\frac{9(n+1)}{2n}+6\end{array}$$

Teorema della media

Il teorema della media dice che, avendo una funzione $f\in C^0:[a,b]\to \mathbb{R}$, allora: $$\exists c\in [a,b]:f(c)=\frac{{\int }_a^{b}f(x)dx}{b-a}$$ dove $(b-a)\cdot f(c)$ può essere pensato come base per altezza.

Teorema fondamentale del calcolo integrale

Se $f:[a,b]\to \mathbb{R}$ continua, allora il teorema produce l'area con segno della funzione $f$: $${\int }_a^{b}f(x)dx=F(b)-F(a)$$

Per esempio, ${\int }_0^2{x}^{2}dx={\left[\frac{x^3}{3}\right]}_0^2=\frac{8}{3}$ dato che $F(x)=\int x^{2}dx-c=\frac{x^3}{3}$.

Oltre a rispettare le proprietà degli integrali indefiniti, rispetta anche la proprietà per cui: $$\left|{\int }_a^{b}f(x)dx\right|\le {\int }_a^b|f(x)|dx$$

Area tra due funzioni

In generale, l'area che tra due funzioni $f(x)$ e $g(x)$ è ricavabile con: $${\int }_a^b|f(x)-g(x)|dx$$

Per esempio, l'area tra le funzioni

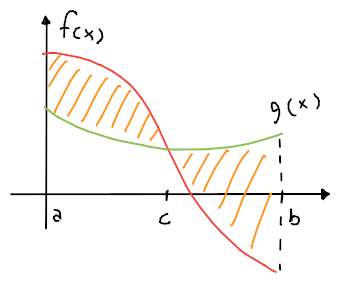
è ricavabile con: $${\int }_a^b|f(x)-g(x)|dx={\int }_a^{c}f(x)-g(x)dx+{\int }_c^{b}g(x)-f(x)dx$$